CAGR: cos’è e come si calcola
Approfondisci cos’è il tasso annuo di crescita composto (CAGR), come si calcola e a cosa serve
FTA Online News, Milano, 29 Set 2022 - 13:30
Il tasso annuo di crescita composto, più comunemente noto come CAGR dall’acronimo anglosassone Compounded Average Growth Rate, rappresenta la crescita percentuale media di una grandezza in un lasso di tempo. Dato per esempio il fatturato A di un’azione all’anno x e il fatturato B di un’azienda nell’anno y, il CAGR dei ricavi indica la crescita percentuale media annua dei ricavi.
Per comprendere il concetto e la sua utilità bisogna partire dal tasso di crescita e dalla sua definizione. Dato un valore iniziale X0 e un valore finale X1, la crescita che si registra tra è dato dalla differenza tra X0 e X1 è ovviamente data dalla differenza X1-X0. Il tasso di crescita “c” sarà invece dato dal rapporto fra crescita e valore iniziale, ossia (X1-X0)/X0 quindi sarà uguale a (X1/X0)-1.
A questo punto torna utile calcolare il valore finale di una grandezza che aumenta con un certo tasso di crescita c quindi (risolvendo l’ultima equazione per X1, ossia il valore finale risultante da un tasso di crescita c) si avrà X1=X0*(c+1).
Se si considerano però più periodi X0, X1, X2, X3, X4, X5… si dovrà ogni volta ricalcolare la crescita sul periodo precedente. La prima volta dunque si avrà X1=X0*(c+1), ma la seconda volta si avrà X2=X1*(c+1), ossia X2=X0*(c+1)*(c+1)=X0*(c+1)^2. La struttura si ripeterà di volta in volta, dando per scontato un tasso di crescita costante, e quindi Xn = X0 * (c+1)^n.
Si tratta di una formula fondamentale in matematica e in economica. Può essere per esempio applicata per calcolare il capitale finale che si ha quando si investe in un’obbligazione a reddito fisso per un numero di anni. Questa formula però consente anche di calcolare a ritroso il nostro tasso annuo di crescita composto CAGR. In questo caso infatti dato il valore finale e quello iniziale, quindi il numero di anni intercorsi, la nostra incognita sarà il tasso di crescita c.
Da ciò dunque
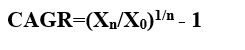
Va evidenziato che il risultato che questa formula fornisce è decimale, quindi per ottenere la variazione percentuale bisognerà moltiplicare il tutto per 100.
CAGR: un esempio di calcolo
Dato un fatturato iniziale di 5 milioni di euro e uno dopo 6 anni di 10 milioni di euro, il CAGR sarà uguale a [(10/5)^1/6]-1, cioè a 0,12246, ossia la società in sei anni avrà mostrato una crescita annua percentuale del 12,24% circa.
Conclusioni
Il CAGR innanzitutto non è un numero “vero”, nel senso che è una media estrapolata, quindi se la crescita media è stata del 5% il secondo anno potrebbe essere stata del 3% o del 7%, ma questo tasso non ci fornisce il dettaglio.
Altra considerazione riguarda l’impiego di questo indicatore: è chiaro che se si prendono in considerazione un anno particolarmente “fiacco” e uno brillante il CAGR mostrerà tassi di crescita assai elevati, che però probabilmente risulteranno meno credibili a un’analisi più approfondita.
Il CAGR è inoltre uno degli indicatori più utilizzati per calcolare il rendimento medio di un investimento in un dato periodo. Anche in questo caso si ottiene una performance media che anno per anno potrà essere stata anche molto distante dal valore ottenuto. Bisogna inoltre evidenziare che se il rendimento di un investimento si è attestato su un valore nel passato, non v’è alcuna garanzia che in futuro si ottenga lo stesso. Il vantaggio indubbio del CAGR è il fatto che dato il valore iniziale e quello finale, oltre ai periodi intercorsi, si ottiene facilmente il rendimento medio annuo e quindi comunque un’indicazione utile.
